មាឌនៃតេត្រាអែត
បើ ជាមាឌរបស់តេត្រាអែតគេបាន
ជាមាឌរបស់តេត្រាអែតគេបាន
 ជាមាឌរបស់តេត្រាអែតគេបាន
ជាមាឌរបស់តេត្រាអែតគេបានដែល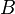 ជាផ្ទៃបាត និង
ជាផ្ទៃបាត និង ជាកំពស់ពីបាតទៅកំពូល ។
ជាកំពស់ពីបាតទៅកំពូល ។
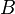 ជាផ្ទៃបាត និង
ជាផ្ទៃបាត និង ជាកំពស់ពីបាតទៅកំពូល ។
ជាកំពស់ពីបាតទៅកំពូល ។ចំពោះតេត្រាអែតដែលមានកំពូល
 និង
និង  គេបាន
គេបាន
 គេបាន
គេបាន
បើគោលតំរុយត្រូវបានជ្រើសរើសនៅ
ត្រង់ នោះ
នោះ  ដូចនេះ
ដូចនេះ
ត្រង់
 នោះ
នោះ  ដូចនេះ
ដូចនេះ

