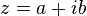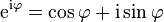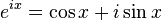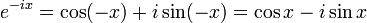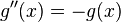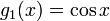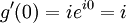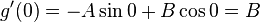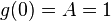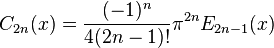ចំនួនកុំផ្លិចដោយសព្វវចនាធិប្បាយសេរីវិគីភីឌា

សាស្រ្ដាចារ្យគណិតក្រិច

គណិតវិទ្យា គឺជាការសិក្សាអំពី បរិមាណ លេខ រចនាសម្ពន័្ធ រូបរាង ហើយនិងការផ្លាស់ប្ដូរ ។ គណិតសាស្រ្ដ អាចជាការស្វែងរកនូវគំរូ ប្រមាណវិធីបង្កើត រូបមន្ដថ្មីៗ ហើយត្រូវបង្កើត អោយពិតប្រាកដ ដោយភាពតឹងរ៉ឹង នាំមកនូវភាពសុចរិត និង មាន អត្ថន័យគ្រប់គ្រាន់ ផងដែរ ។
យើងអាចនិយាយបាន ផងដែរថា៖ គណិតសាស្រ្ដ គឺជាមុខរបររបស់ មនុស្សគ្រប់គ្នា ដែលយើងត្រូវតែរៀន ហើយមនុស្សជាច្រើន បានរកឃើញ នូវវត្ថុផ្សេង ៗ
ដើម្បីជួយសំរួលដល់ ការងារប្រចាំថ្ងៃ បានយ៉ាងប្រសើរបំផុត ទៀតផង ។ ផ្នែកដែលសំខាន់បំផុត របស់គណិតវិទ្យានោះគឺ

សំរាប់ដោះស្រាយ បញ្ហាជាច្រើន ដែលកើតមានទើ្បង ក្នុងពិភពលោកយើងនេះ បានយ៉ាងប្រពៃ ដូចជា ការគណនា បូក ដក គុណ ចែក ទាំងអស់នេះ សុទ្ធតែត្រូវការ គណិតវិទ្យា ទាំងអស់ ។
ដូច្នេះហើយ បានជាមនុស្សជាច្រើន តែងចូលចិត្ដសិក្សា និង ប្រើគណិតវិទ្យា ។
សព្វថ្ងៃនេះ ការងារមួយចំនួនដូចជា ជំនួញ វិទ្យាសាស្រ្ដ វិស្វករ និងសំនង់ ។

កុំផ្លិចឆ្លាស់

ធរណីមាត្រនៃ $z \,$ $\bar{z} \,$ ក្នុងប្លង់កុំផ្លិច និងកុំផ្លិចឆ្លាស់របស់វា

ក្នុងគណិតវិទ្យា កុំផ្លិចឆ្លាស់(complex conjugate) នៃចំនួនកុំផ្លិចត្រូវបានផ្តល់អោយដោយការប្តូរសញ្ញានៃផ្នែកនិម្មិត។

និយមន័យ

ចំនួនកុំផ្លិចឆ្លាស់នៃចំនួនកុំផ្លិច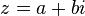 $z = a + bi\,$ , ដែលa និងb
ជាចំនួនពិត គេបាន $\bar{z} = a - bi\,$ ។ ហើយ $\bar z \,$ អានថា $z\,$ បារ។
ម៉ូឌុលនៃចំនួនកុំផ្លិចឆ្លាស់រក្សាតំលៃស្មើនឹង
ចំនួនកុំផ្លិចរបស់វា មិនផ្លាស់ប្តូរទេ ( $\left| \overline{z} \right| = \left| z \right|$ ) ។

$\begin{array}{r|ccc} c:& \mathbb{C} & \longrightarrow & \mathbb{C} \\ & z & \longmapsto & \overline{z} \end{array}$

ដូច្នេះកុំផ្លិចឆ្លាស់នៃចំនួនកុំផ្លិច

$z=a+ib \,$

(ដែល

a

និង

b

ជាចំនួនពិត)គឺ

$\overline{z} = a - ib\,$

ជាទូទៅ កុំផ្លិចឆ្លាស់ត្រូវបានគេតាងដោយ $\bar{z} \,$ ឬ $z^*\,$ ។
ឧទាហរណ៍

$\overline{(3-2i)} = 3 + 2i$
$\overline{7}=7$
$\overline{i} = -i$

ជាទូទៅគេគិតពីចំនួនកុំផ្លិចជាចំនុចនៅក្នុងប្លង់
កុំផ្លិចជាមួយប្រព័ន្ធកូអរដោនេដេកាត។
អ័ក្សអាប់ស៊ីស $x\,$ តំណាងអោយផ្នែកពិត
និងអ័ក្សអរដោនេ $y\,$ ផ្នែកនិម្មិតដែលរួមមានឯកតានិម្មិត $i \,$ ។
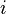ក្នុងទំរង់ប៉ូលែរកុំផ្លិចឆ្លាស់នៃ $r e^{i \phi} \,$ គឺ $r e^{-i \phi} \,$ ។
រូបមន្តនេះត្រូវបានផ្ទៀតផ្ទាត់ដោយរូបមន្តអឺលែរ។
ចំនែកឯក្នុងទំរង់ត្រីកោណមាត្រវិញ បើ
$z = r (\cos \theta + i \sin \theta)\,$ នោះផ្នែកពិតនៃ $z \,$ គឺ $r \cos \theta \,$ ។

$z=a+b\,\mathrm{i}\in\Bbb C$ $a = \mathrm{Re}(z) = \frac12 ( z + \bar z)$ ជាទូទៅបើ គេបាន:

$z \cdot\bar z = |z|^2 = a^2+b^2$

$b = \mathrm{Im}(z) = \frac{1}{2\mathrm{i}} ( z - \bar z )$

លក្ខណៈនៃកុំផ្លិចឆ្លាស់

គេមានគ្រប់ចំនួនកុំផ្លិច

z

និង

w

ក) $\overline{(z + w)} = \overline{z} + \overline{w} \!\$

ខ) $\overline{(z - w)} = \overline{z} - \overline{w} \!\$

គ) $\overline{(zw)} = \overline{z}\; \overline{w} \!\$

ឃ) $\overline{\left({\frac{z}{w}}\right)} = \frac{\overline{z}}{\overline{w}}$ បើ

w

មិនសូន្យ

ង) $\overline{z} = z \!\$ ប្រសិនបើ

z

ជាចំនួនពិតសុទ្ធ

ច) $\overline{z^n} = \overline{z}^n$ គ្រប់ចំនួនគត់រឺឡាទីប

n

ឆ) $\left| \overline{z} \right| = \left| z \right|$

ជ) ${\left| z \right|}^2 = z\overline{z} = \overline{z}z$

ឈ) $z^{-1} = \frac{\overline{z}}{{\left| z \right|}^2}$ បើ

z

មិនសូន្យ

ញ) $\left(\overline { e^{z}} \right) = e^{\overline z}$

ដ) $\left(\overline { \sin {z}} \right) = \sin \overline z$

ឋ) $\left(\overline { \cos {z}} \right) = \cos \overline z$

ឌ) $\left(\overline { \sinh {z}} \right) = \sinh \overline z$

ត្រីកោណមាត្រកុំផ្លិច

អនុគមន៍ត្រីកោណមាត្រ

ក្នុងចំនួនកុំផ្លិច រូបមន្តអឺលែរចំពោះអនុគមន៍ត្រីកោណមាត្រអាចកំនត់

$\sin z = \frac {e^{iz} - e^{-iz}} {2i} = \frac {\sinh iz} {i} = \sum _{k=0}^{\infty}{\frac {(-1)^k z^{2k+1}} {(2k+1)!}}$

$\cos z = \frac {e^{iz} + e^{-iz}} {2} = {\cosh iz} = \sum _{k=0}^{\infty}{\frac {(-1)^k z^{2k}} {(2k)!}}$

$\tan z = \frac {\sin z} {\cos z} = -i \frac {\sinh iz} {\cosh iz} = -i \tanh iz = -i \frac {e^{iz} - e^{-iz}} {e^{iz} + e^{-iz}}$

ដូចគ្នាចំពោះអនុគមន៍ត្រីកោណមាត្រច្រាស់

$\arcsin z = -i \ln \left( i z + \sqrt { 1-z^2} \right)$
$\arccos z = -i \ln \left( z + \sqrt {z^2-1} \right)$
$\arctan z = \frac i 2 \Big( \ln(1 - iz) - \ln(1+iz) \Big)$

អនុគមន៍ត្រីកោណមាត្រកុំផ្លិច

ខាងក្រោមនេះជាបំណកស្រាយនៃរូបមន្តសំរាប់គណនាកូស៊ីនុសនៃចំនួនកុំផ្លិច

$af + ibf = \cos{(a + i.b)} = \frac{e^{i(a + i.b)} + e^{-i(a + i.b)}} {2} = \frac{e^{i.a - b} + e^{-i.a + b}}{2} = \frac{e^{-b}.e^{i.a} + e^{b}.e^{-i.a}}{2} = \frac{e^{-b}}{2}.e^{i.a} + \frac{e^{-b}}{2}.e^{-i.a}$

$\Rightarrow r_1 = \frac{e^{-b}}{2}$ $t_1 = a \,$ $\Rightarrow r_2 = \frac{e^{b}}{2}$ $t_2 = -a \,$

$\Rightarrow a_1 = r_1.\cos{t_1} = \frac{e^{-b}}{2}.\cos{a}$ $b_1 = r_1.\sin{t_1} = \frac{e^{-b}}{2}.\sin{a}$

$\Rightarrow a_2 = r_2.\cos{t_2} = \frac{e^{b}}{2}.\cos{(-a)} = \frac{e^{b}}{2}.\cos{a}$ $b_2 = r_2.\sin{t_2} = \frac{e^{b}}{2}.\sin{(-a)} = -\frac{e^{b}}{2}.\sin{a}$

$\Rightarrow af = a_1 + a_2 = \frac{e^{-b}}{2}.\cos{a} + \frac{e^{b}}{2}.\cos{a} = \cos{a}.[\frac{e^{-b}}{2} + \frac{e^{b}}{2}] = \cos{a}.[\frac{e^{b} + e^{-b}}{2}] = \cos{a}.\cosh{b}$

$=> bf = b_1 + b_2 = \frac{e^{-b}}{2}.\sin{a} - \frac{e^{b}}{2}.\sin{a} = \sin{a}.[\frac{e^{-b}}{2} - \frac{e^{b}}{2}] = \sin{a}.[\frac{-1.(e^{b} - e^{-b})}{2}] = -\sin{a}.\sinh{b}$

$\Rightarrow \cos{(a + i.b)} = \cos{(a)}.\cosh{(b)} - i.\sin{(a)}.\sinh{(b)} \,$

ចំពោះអនុគមន៍ត្រីកោណមាត្រផ្សេងទៀត ក៏ដូចគ្នាដែរ។

$\tan{z} = \frac{\sin{z}}{\cos{z}}$ $\cot{z} = \frac{\cos{z}}{\sin{z}}$

សូមមើលផងដែរចំពោះសំរាយបញ្ជាក់នៃកូស៊ីនុសអ៊ីពែបូលីក

$af + ibf = \cosh{(a + i.b)} = \frac{e^{a + i.b} + e^{-(a + i.b)}} {2} = \frac{e^{a + i.b} + e^{-a - i.b}}{2} = \frac{e^{a}.e^{i.b} + e^{-a}.e^{-i.b}}{2} = \frac{e^{a}}{2}.e^{i.b} + \frac{e^{-a}}{2}.e^{-i.b}$

$=> r_1 = \frac{e^{a}}{2}$ $t_1 = b \,$ $=> r_2 = \frac{e^{-a}}{2}$ $t_2 = -b \,$

$=> a_1 = r_1.\cos{t_1} = \frac{e^{a}}{2}.\cos{b}$ $b_1 = r_1.\sin{t_1} = \frac{e^{a}}{2}.\sin{b}$

$=> a_2 = r_2.\cos{t_2} = \frac{e^{-a}}{2}.\cos{(-b)} = \frac{e^{-a}}{2}.\cos{b}$ $b_2 = r_2.\sin{t_2} = \frac{e^{-a}}{2}.\sin{(-b)} = -\frac{e^{-a}}{2}.\sin{b}$

$=> af = a_1 + a_2 = \frac{e^{a}}{2}.\cos{b} + \frac{e^{-a}}{2}.\cos{b} = [\frac{e^{a}}{2} + \frac{e^{-a}}{2}].\cos{b} = [\frac{e^{a} + e^{-a}}{2}].\cos{b} = \cosh{a}.\cos{b}$

$=> bf = b_1 + b_2 = \frac{e^{a}}{2}.\sin{b} - \frac{e^{-a}}{2}.\sin{b} = [\frac{e^{a}}{2} - \frac{e^{-a}}{2}].\sin{b} = [\frac{e^{a} - e^{-a}}{2}].\sin{b} = \sinh{a}.\sin{b}$

$=> \cosh{(a + i.b)} = \cosh{(a)}.\cos{(b)} - i.\sinh{(a)}.\sin{(b)} \,$

ដូចគ្នាដែរចំពោះអនុគមន៍អ៊ីពែបូលីកផ្សេងទៀត

$\tanh{z} = \frac{\sinh{z}}{\cosh{z}}$ $\coth{z} = \frac{\cosh{z}}{\sinh{z}}$

រូបមន្តដឺម័រ

ដោយសព្វវចនាធិប្បាយសេរីវិគីភីឌា

លោតទៅ៖ ទិសដៅ, ស្វែងរក

រូបមន្តដឺម័រ (De Moivre's formula) ត្រូវបានគេហៅដោយយក
តាមឈ្មោះរបស់លោក អាប្រាហាម ដឺ ម័រ (Abraham de Moivre) ដែលជាជនជាតិបារាំង ដោយបានចែងថាចំពោះគ្រប់ចំនួនកុំផ្លិច (និងជាពិសេសចំពោះគ្រប់ចំនួនពិត)
x និង គ្រប់ចំនួនគត់ n គេបាន

ការទាញយករូបមន្តដឺម័រ

រូមមន្តដឺម័រអាចត្រូវបានទាញចេញដោយងាយដោយប្រើរូបមន្តអយល័រ

$e^{ix} = \cos x + i\sin x\,$

និងតាមទ្រឹស្តីបទអិចស្ប៉ូណង់ស្យែល

$\left( e^{ix} \right)^n = e^{inx} \,$ ។

តាមរូបមន្តអយល័រ គេបាន

$e^{i(nx)} = \cos(nx) + i\sin(nx) \,$ ។

សំរាយបញ្ជាក់រូបមន្ត

គេមាន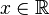 $x\in\mathbb{R}$
យើងសិក្សា៣ករណី
(១). ករណី $n>0 \,$ យើងបកស្រាយប្រើវិចារកំនើន។
នៅពេល 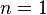$n = 1 \,$ លទ្ធផលគឺពិតជាត្រឹមត្រូវ។
តាមសម្មតិកម្ម យើងសន្មតថាលទ្ធផលគឺពិតចំពោះគ្រប់ចំនួនគត់វិជ្ជមាន $k \,$ គឺថា

$\left(\cos x + i \sin x\right)^k = \cos\left(kx\right) + i \sin\left(kx\right) \,$

យើងបាន

ចំពោះ $n=1 ; \quad \Rightarrow (\cos x + i \sin x)^1 = \cos (1 \cdot x) + i \sin (1 \cdot x) \qquad \,$ ពិត
ចំពោះ $n=2 \,;$
$\begin{align} \Rightarrow (\cos x + i \sin x)^2 &= \cos^2 x -\sin^2 x + 2i \cos x \sin x \\ &=\cos (2 \cdot x) + i \sin (2 \cdot x) \qquad \\ \end{align}$
សមីការផ្ទៀងផ្ទាត់ចំពោះ n = 2 ដែរ

ឧបមាថាវាពិតដល់ $n=k+1 \;$ គេបាន

$\begin{alignat}{2} \left(\cos x+i\sin x\right)^{k+1} & = \left(\cos x+i\sin x\right)^{k} \left(\cos x+i\sin x\right)\\ & = \left[\cos\left(kx\right) + i\sin\left(kx\right)\right] \left(\cos x+i\sin x\right) &&\qquad \\ & = \cos \left(kx\right) \cos x - \sin \left(kx\right) \sin x + i \left[\cos \left(kx\right) \sin x + \sin \left(kx\right) \cos x\right]\\ & = \cos \left[ \left(k+1\right) x \right] + i\sin \left[ \left(k+1\right) x \right] &&\qquad \end{alignat}$

យើងសន្និដ្ឋានថាលទ្ធផលពិតចំពោះ $n = k + 1 \,$ នៅពេលដែល $n = k \,$ ។ តាមគោលការណ៍វិចារកំនើនគណិតវិទ្យា
លទ្ធផលពិតចំពោះគ្រប់ចំនួនគត់វិជ្ជមាន $n \ge 1 \,$
(២). ករណី $n = 0 \,$ រូបមន្តពិតព្រោះ
$\cos (0x) + i\sin (0x) = 1 + i0 = 1 \,$ , គេអាចសន្មត

z 0 = 1

។
(៣). ករណី $n < 0 \,$ យើងសន្មតមានចំនួនពិតវិជ្ជមាន $m \,$ ដែល $n = -m \,$ ។ ដូចនេះ

$\begin{align} \left(\cos x + i\sin x\right)^{n} & = \left(\cos x + i\sin x\right)^{-m}\\ & = \frac{1}{\left(\cos x + i\sin x\right)^{m}}\\ & = \frac{1}{\left(\cos mx + i\sin mx\right)}\\ & = \cos\left(mx\right) - i\sin\left(mx\right)\\ & = \cos\left(-mx\right) + i\sin\left(-mx\right)\\ & = \cos\left(nx\right) + i\sin\left(nx\right) \end{align}$

ដូចនេះរូបមន្តពិតចំពោះគ្រប់តំលៃជាចំនួនគត់នៃ n ។

[កែប្រែ] លក្ខណៈទូទៅ

ប្រសិនបើ z និង w' គឺជាចំនួនកុំផ្លិច នោះគេបាន

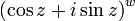
$\left(\cos z + i\sin z\right)^w$

គឺជាអនុគមន៍មានតំលៃច្រើន ដែល

$\cos (wz) + i \sin (wz)\,$

មិនមែន។ ដូចនេះគេអាចពោលថា

$\cos (wz) + i \sin (wz) \,$ គឺជាតំលៃមួយនៃ $\left(\cos z + i\sin z\right)^w \,$

គំនូសមនៅលើ ប្លង់កុំផ្លិចនៃរឹសគូបនៃ១

អនុវត្ត

រូបមន្តនេះអាចត្រូវបានគេប្រើប្រាស់ដើម្បី
រករឹសទី n នៃចំនួនកុំផ្លិច។ ប្រសិនបើ z ជាចំនួនកុំផ្លិច សរសេរក្នុងទំរង់ប៉ូលែរជា

$z=r\left(\cos x+i\sin x\right) \,$

គេបាន

$z^{{}^{\frac{1}{n}}}= \left[ r\left( \cos x+i\sin x \right) \right]^ {{}^{\frac{1}{n}}}= r^{{}^{\frac{1}{n}}} \left[ \cos \left( \frac{x+2k\pi}{n} \right) + i\sin \left( \frac{x+2k\pi}{n} \right) \right]$

រូបមន្តអយល័រ

ដោយសព្វវចនាធិប្បាយសេរីវិគីភីឌា

លោតទៅ៖ ទិសដៅ, ស្វែងរក

រូបមន្តអយល័រ $\mathrm e^{\mathrm i\varphi}=\cos\varphi+\mathrm i\sin\varphi$

រូបមន្តអយល័រ (Euler's formula) យកឈ្មោះតាមលោក
លេអូណា អយល័រ (Leonhard Euler) គឺជារូបមន្តគ
ណិតវិទ្យាក្នុងការគណនាកុំផ្លិចដែលបង្ហាញទំនាក់
ទំនងយ៉ាងជិតស្និតរវាងអនុគមន៍ត្រីកោណមាត្រ និង
អនុគមន៍អិចស្ប៉ូណង់ស្យែលកុំផ្លិច។
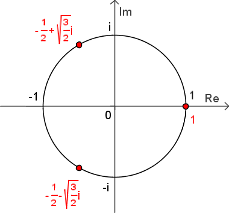
រូបមន្តអយល័រពោលថាចំពោះគ្រប់ចំនួនពិត $\ x$ គេបាន

$\color{blue} e^{ix} = \cos x + i\;\sin x$

ដែល

$\ e$ គឺជាគោលនៃលោការីតនេពែ (លោការីតធម្មជាតិ)
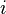$\ i$ គឺជាឯកតានិម្មិត (ឬហៅថាចំនួននិម្មិត)
$\ \sin$ និង $\ \cos$ គឺជាអនុគមន៍ត្រីកោណមាត្រ

រូបមន្តអយល័រនៅតែពិតបើទោះបីជា $\ x$ ជាចំនួនកុំផ្លិចក៏ដោយ។

ប្រវត្តិ

រូបមន្តអយល័រត្រូវបានស្រាយបញ្ជាក់ដំបូងដោយ
រ៉ូចឺ កូត្ស Roger Cotes ក្នុងឆ្នាំ ១៧១៤ ជារាង

$\ln(\cos x + i\sin x)=ix \$

(ដែល ln តំណាងអោយលោការីតនេពែ
(ឬហៅម្យ៉ាងទៀតថាលោការីតធម្មជាតិ)
មានន័យថាជាលោការីត log ដែលមានគោល e)
លោកអយល័រជាអ្នកបោះពុម្ពរូបមន្តជារាង
បច្ចប្បន្ននេះនៅឆ្នាំ១៧៤៨ ដែលជាមូលដ្ឋាន
គ្រឹះសំរាប់សំរាយបញ្ជាក់របស់គាត់ចំពោះ
ស៊េរីអនន្តពីរស្មើគ្នា។ អ្នកទាំងពីរមិនបាន
បង្ហាញតំណាងធរណីមាត្រនៃរូបមន្តទេៈ
តំណាងនៃចំនួនកុំផ្លិចជាចំនុចនៅក្នុងប្លង់កុំផ្លិច
បានលេចឡើងនៅ៥០ឆ្នាំក្រោយមក។
លោក អយល័របានចាត់ទុកវាជាធម្មតាដើម្បីណែនាំឮ
ទៅកាន់សិស្សរបស់គាត់អំពីចំនួនកុំផ្លិចមានភាព
ស្រួលច្រើនជាងអ្វីដែលពួកយើងធ្វើសព្វថ្ងៃ។
នៅក្នុងសៀវភៅពិជគណិតថ្នាក់ដំបូងរបស់គាត់
(elementary algebra text book) គាត់បានណែនាំ
អំពីចំនួនទាំងនេះយ៉ាងហោចណាស់ម្តង និង
បានប្រើប្រាស់ពួកវាតាមរយៈវិធីសាស្រ្តធម្មតា។

[កែប្រែ] ការអនុវត្តន៍ក្នុងទ្រឹស្តីចំនួនកុំផ្លិច

$\ e^{ix}$ គូសជារង្វង់ត្រីកោណមាត្រក្នុងប្លង់កុំផ្លិច

រូបមន្តនេះអាចត្រូវបានគេបកស្រាយដោយ
និយាយថា អនុគមន៍ $\ e^{ix}$ គូសជារង្វង់ត្រីកោណមាត្រក្នុងប្លង់កុំផ្លិចជា $\ x$ រ៉ាដ្យង់
តាមរយះចំនួនពិត ។ ទីនេះ $\ x$ គឺជាមុំដែលបន្ទាត់មួយភ្ជាប់
គល់តំរុយជាមួយចំនុចមួយនៅលើ
រង្វង់ត្រីកោណមាត្របង្កើតជាមួយអ័ក្ស
ពិតផ្នែកវិជ្ជមានតាមទិសដៅដូចទ្រនិចនាឡិកានិងគិតជារ៉ាដ្យង់។
សំរាយបញ្ជាក់ដើមគឺពឹងផ្អែកទៅលើការពន្លាតជា
ស៊េរីតេល័រនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែល $\ e^z$
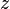(ដែល $\ z$ ជាចំនួនកុំផ្លិច) និងការពន្លាតជា
ស៊េរីតេល័រនៃអនុគមន៍ស៊ីនុស $\ \sin x$ និង
កូស៊ីនុស $\ \cos$ ចំពោះចំនួនពិត $\ x$ ។
តាមពិតសំរាយបញ្ជាក់ដូចគ្នាបង្ហាញថារូបមន្ត
អយល័រពិតផងដែរចំពោះគ្រប់ចំនួនកុំផ្លិច $\ z$ ។
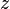ចំនុចមួយនៅក្នុងប្លង់កុំផ្លិចអាចត្រូវបានបង្ហាញជា
ចំនួនកុំផ្លិចដៅក្នុងប្រព័ន្ធកូអរដោនេដេកាត។
រូបមន្តអយល័រផ្តល់នូវតំលៃមធ្យមនៃគំលាតរវាង
កូអរដោនេដេកាត និង កូអរដោនេប៉ូលែរ។
ទំរង់ប៉ូលែរបន្ថយចំនួណតួពីពីរទៅមួយ
ដែលសំរួលក្នុងគណិតវិទ្យានៅពេលដែលវា
ត្រូវបានគេប្រើប្រាស់ក្នុង ប្រមាណវិធីគុណ
ឬស្វ័យគុណនៃចំនួនកុំផ្លិច។ ចំនួនកុំផ្លិច $\ z = x + iy$ អាចសរសេរជា

$z = x + iy = |z| (\cos \theta+ i\sin \theta) = |z| e^{i \theta}= r e^{i \theta} \,$

$\bar{z} = x - iy = |z| (\cos \theta- i\sin \theta) = |z| e^{-i \theta}= r e^{-i \theta} \,$

ដែល

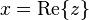$x = \mathrm{Re}\{z\} \,$ គឺជាផ្នែកពិត

$y = \mathrm{Im}\{z\} \,$ គឺជាផ្នែកនិម្មិត

$|z| = r = \sqrt{x^2+y^2}$ គឺជាម៉ូឌុលនៃចំនួនកុំផ្លិច

$\ \bar{z}$ ជាចំនួនកុំផ្លិចឆ្លាស់នៃ $\ z$

$\theta= \arctan (\frac{y}{x})$ គឺជាអាគុយម៉ង់នៃចំនួនកុំផ្លិច

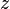
$\ \theta$ គឺជាអាគុយម៉ងនៃចំនួនកុំផ្លិច
មានន័យថាគឺជាមុំរវាងអ័ក្សពិត $\ x$ និង វ៉ិចទ័រ $\ z$
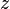
វាស់ក្នុងទិសដៅស្របនឹងទ្រនិចនាឡិកានិងគិតជារ៉ាដ្យង់។
យើងអាចប្រើរូបមន្តអយល័រដើម្បីកំនត់លោការីតនៃចំនួនកុំផ្លិចមួយ។
យើងក៏អាចប្រើនិយមន័យនៃលោការីត (ជាឆ្លាស់នៃអិចស្ប៉ូណង់ស្យែល) ដែល

$a = e^{\ln (a)}\,$

និង

$e^a e^b = e^{a + b}\,$

ទំនាក់ទំនងទាំងពីរពិតចំពោះគ្រប់ចំនួនកុំផ្លិច a និង b ។
ហេតុនេះយើងអាចសរសេរ

$z = |z| e^{i \theta} = e^{\ln |z|} e^{i \theta} = e^{\ln |z| + i \theta}\,$

ចំពោះ $z\ne 0$ ។ បំលាក់លោការីតលើអង្គទាំងសងខាង យើងបាន

$\ln z= \ln |z| + i \theta \,$

តាមពិតទំនាក់ទំនងនេះអាចត្រូវបានគេប្រើ
ដើម្បីកំនត់និយមន័យសំរាប់កុំផ្លិចលោការីត។ លោការីតនៃចំនួនកុំផ្លចមួយគឺជា
អនុគមន៍មានពហុតំលៃ ពីព្រោះ $\theta \,$ មានពហុតំលៃ (មានតំលៃច្រើន) ។
ចុងក្រោយ រូបមន្តអិចស្ប៉ូណង់ស្យែល

$(e^a)^k = e^{a k} \,$

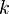ផ្ទៀងផ្ទាត់ចំពោះគ្រប់ចំនួនគត់ $\ k$ រួមជាមួយរូបមន្តអយល័រ ដែលជាប់ទាក់ទងផងដែរនូវរូបមន្តត្រីកោណមាត្រ និង រូបមន្តដឺម័រ។

ទំនាក់ទំនងចំពោះត្រីកោណមាត្រ

$\cos x = \mathrm{Re}\{e^{ix}\} ={e^{ix} + e^{-ix} \over 2}$

$\sin x = \mathrm{Im}\{e^{ix}\} ={e^{ix} - e^{-ix} \over 2i}$

សមីការទាំងពីរខាងលើអាចទាញបានដោយការបូកឬដករូបមន្តអយល័រ៖

$e^{ix} = \cos x + i \sin x \;$

$e^{-ix} = \cos(- x) + i \sin(- x) = \cos x - i \sin x \;$

រូបមន្តទាំងនេះផ្តល់និយមន័យអោយ
អនុគមន៍ត្រីកោណមាត្រចំពោះអាគុយម៉ង់ $\ x$ នៃចំនួនកុំផ្លិច ។
ឧទាហរណ៍៖ តាង $\ x = iy$ គេបាន

$\cos(iy) = {e^{-y} + e^{y} \over 2} = \cosh(y)$

$\sin(iy) = {e^{-y} - e^{y} \over 2i} = -i\sinh(y)$

អិចស្ប៉ូណង់ស្យែលកុំផ្លិចអាចសំរួលជាត្រីកោណមាត្រ ពីព្រោះវាងាយស្រួលសំរួលជាងស៊ីនុយសូអ៊ីត។ គេអាចបំលែងស៊ីនុយសូអ៊ីតជាកន្សោមអិចស្ប៉ូណង់ស្យែល។ ឧទាហរណ៍៖

$\begin{align} \cos x\cdot \cos y & = \frac{(e^{ix}+e^{-ix})}{2} \cdot \frac{(e^{iy}+e^{-iy})}{2} \\ & = \frac{e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{4} \\ & = \frac{e^{i(x+y)}+e^{i(-x-y)}}{4}+\frac{e^{i(x-y)}+e^{i(-x+y)}}{4} \\ & = \frac{\cos(x+y)}{2} + \frac{\cos(x-y)}{2} \end{align}$

គេអាចបំលែងស៊ីនុយសូអ៊ីតជាផ្នែកពិតនៃកន្សោមចំនួនកុំផ្លិច និង សរសេរជាកន្សោមនៃចំនួនកុំផ្លិច។ ឧទាហរណ៍៖

$\begin{align} \cos(nx)+\cos((n-2)x) & = \mathrm{Re} \{\quad e^{inx}+e^{i(n-2)x}\quad \} \\ & = \mathrm{Re} \{\quad e^{i(n-1)x}\cdot (e^{ix}+e^{-ix})\quad \} \\ & = \mathrm{Re} \{\quad e^{i(n-1)x}\cdot 2\cos x\quad \} \\ & = 2\cos((n-1)x)\cos x \end{align}$

រូបមន្តនេះត្រូវបានគេប្រើប្រាស់ដើម្បីបង្កើតរបត់ស៊ីនុយសូអ៊ីតនៅចន្លោះ x រ៉ាដ្យង់។

សំរាយបញ្ជាក់

សំរាយបញ្ជាក់ដោយប្រើស៊េរីតេល័រ

ការពន្លាតជាស៊េរីនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែល
ដែលមានអថេរជាចំនួនពិត x អាចសរសេរ

$e^x = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + ... = \sum_{n=0}^\infty \frac{x^n}{n!}$

និងអាចបន្លាយដល់ចំនួនកុំផ្លិច x ។
ពន្លាតជាស៊េរីតេល័រចំពោះអនុគមន៍ស៊ីនុស និង កូស៊ីនុសគឺ

$\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}$

ដើម្បីសំរួលសមីការនេះ យើងប្រើលក្ខណៈគ្រឹះខាងក្រោម

$i^0 = 1, \qquad i^1 = i, \qquad i^2 = -1, \qquad i^3 = -i, \qquad i^4 = 1, \ldots$

ជាទូទៅចំពោះគ្រប់អិចស្ប៉ូសង់ជាចំនួនគត់ n គេបាន

$i^{\,4n} = 1, \qquad i^{\,4n+1} = i, \qquad i^{\,4n+2} = -1, \qquad i^{\,4n+3} = -i$

ចំពោះចំនួនកុំផ្លិច z យើងកំនត់អនុគមន៍និមួយៗ
ទាំងនេះដោយស៊េរីខាងលើ ជំនួសអថេរពិត x ដោយអថេរកុំផ្លិច z ។ យើងបាន

$\begin{align} e^{iz} &{}= 1 + iz + \frac{(iz)^2}{2!} + \frac{(iz)^3}{3!} + \frac{(iz)^4}{4!} + \frac{(iz)^5}{5!} + \frac{(iz)^6}{6!} + \frac{(iz)^7}{7!} + \frac{(iz)^8}{8!} + \cdots \\ &{}= 1 + iz - \frac{z^2}{2!} - \frac{iz^3}{3!} + \frac{z^4}{4!} + \frac{iz^5}{5!} - \frac{z^6}{6!} - \frac{iz^7}{7!} + \frac{z^8}{8!} + \cdots \\ &{}= \left( 1 - \frac{z^2}{2!} + \frac{z^4}{4!} - \frac{z^6}{6!} + \frac{z^8}{8!} - \cdots \right) + i\left( z - \frac{z^3}{3!} + \frac{z^5}{5!} - \frac{z^7}{7!} + \cdots \right) \\ &{}= \cos z + i\sin z \end{align}$

ដូចនេះគេបានរូបមន្តអយល័រ ដូចដែលបានពោល៖

$\color{blue} e^{ix} = \cos x + i\;\sin x$

សំរាយបញ្ជាក់ដោយប្រើដេរីវេ

គេមានអនុគមន៍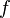 $\ f$ (អាចជាអនុគមន៍ចំនួនកុំផ្លិច) នៃអថេរ x កំនត់ដោយ

$f(x) = \frac{\cos x+i\sin x}{e^{ix}} \$

ដោយយោងតាមរូបមន្តផលគុណ និង ផលចែកនៃ
ដេរីវេនៃអនុគមន៍ 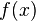$\ f(x)$ គេបានដេរីវេនៃអនុគមន៍ 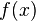$\ f(x)$ កំនត់ដោយ
$\begin{align} f'(x) &= \displaystyle\frac{(-\sin x+i\cos x)\cdot e^{ix} - (\cos x+i\sin x)\cdot i\cdot e^{ix}}{(e^{ix})^2} \\ &= \displaystyle\frac{-\sin x\cdot e^{ix}-i^2\sin x\cdot e^{ix}}{(e^{ix})^2} \\ &= \displaystyle\frac{-\sin x-i^2\sin x}{e^{ix}} \\ &= \displaystyle\frac{-\sin x-(-1)\sin x}{e^{ix}} \\ &= \displaystyle\frac{-\sin x+\sin x}{e^{ix}} \\ &= 0 \end{align}$
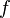ហេតុនេះ $\ f$ ជាអនុគមន៍ថេរ។ គេបាន

$f(x)=f(0)=\frac{\cos 0 + i \sin 0}{e^0}=1$

$\Rightarrow \frac{\cos x + i \sin x}{e^{ix}}=1$

ដូចនេះ

$\color{blue} e^{ix} = \cos x + i\;\sin x$

[កែប្រែ] សំរាយបញ្ជាក់ដោយប្រើសមីការឌីផេរ៉ង់ស្យែល

គេមានអនុគមន៍ $\ g(x)$ ដែល

$\ g(x) = e^{ix}$

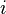ដោយចាត់ទុក $\ i$ គឺជាចំនួនថេរ ដេរីវេទី១ និង ទី២ នៃ $\ g(x)$ គឺ

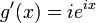
$g'(x) = i e^{ix} \$

$g''(x) = i^2 e^{ix} = -e^{ix} \$ (ពីព្រោះ $\ i^2 = -1$ )

ចេញពីទំនាក់ទំនងនេះគេអាចបង្កើតសមីការឌីផេរ៉ង់ស្យែលលីនែអ៊ែរលំដាប់២

$g''(x) = -g(x) \$

ឬ

$g''(x) + g(x) = 0 \$

សមីការឌីផេរ៉ង់ស្យែលលីនេអ៊ែរលំដាប់២ មានចំលើយឯករាជ្យ
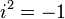លីនេអ៊ែរចំនួនពីរដែលផ្ទៀងផ្ទាត់វា៖

$g_1(x) = \cos x \$

$g_2(x) = \sin x \$

ទាំង $\ \cos$ និង $\ \sin$ គឺជាអនុគមន៍ពិតដែលដេរីវេទី២គឺ
មានសញ្ញាអវិជ្ជមាននៃអនុគមន៍ខ្លួនវា។ បន្សំលីនេអ៊ែរនៃចំលើយចំពោះសមីការឌីផេរ៉ង់ស្យែលអូម៉ូសែនក៏ជាចំ
លើយមួយផងដែរ។ ចំលើយទូទៅនៃសមីការគឺ

$\begin{align} g(x) &= A g_1(x) + B g_2(x) \\ &= A \cos x + B \sin x \ \end{align}$

ដែល A និង B គឺជាចំនួនថេរ។ ប៉ុន្តែមិនមែនគ្រប់តំលៃទាំង
អស់នៃចំនួនថេរទាំងពីរនេះសុទ្ធតែផ្ទៀងផ្ទាត់លក្ខខណ្ឌ
ដើមដែលគេស្គាល់ចំពោះ $\ g(x)$ ទេ៖

$g(0) = e^{i0} = 1 \$

$g'(0) = i e^{i0} = i \$

តំលៃនៃលក្ខខណ្ឌដើមជំនួសក្នុងចំលើយទូទៅ

$g(0) = A \cos 0 + B \sin 0 = A \$

$g'(0) = -A \sin 0 + B \cos 0 = B \$

គេបាន

$g(0) = A = 1 \$

$g'(0) = B = i \$

និងចុងក្រោយ

ម៉ាទ្រីសប្រាម៉ាហ្គឹបតា

ដោយសព្វវចនាធិប្បាយសេរីវិគីភីឌា

លោតទៅ៖ ទិសដៅ, ស្វែងរក

ម៉ាទ្រីសខាងក្រោមនេះគឺត្រូវបានរកឃើញដោយលោក ប្រាម៉ាហ្គឹបតា(Brahmagupta)ដែលជាគណិតវិទូជាតិឥណ្ឌា នៅឆ្នាំ៦២៨ ។

$B(x,y) = \begin{bmatrix} x & y \\ \pm ty & \pm x \end{bmatrix}\,$

វាផ្តល់អោយ

$B(x_1,y_1) B(x_2,y_2) = B(x_1 x_2 \pm ty_1 y_2,x_1 y_2 \pm y_1,x_2)\,$

ស្វ័យគុណនៃម៉ាទ្រីសគឺកំនត់ដោយ

$B^n = \begin{bmatrix} x & y \\ ty & x \end{bmatrix}^n = \begin{bmatrix} x_n & y_n \\ ty_n & x_n \end{bmatrix} \equiv B_n\,$

$\ x_n$ និង $\ y_n$ ហៅថាពហុធាប្រាម៉ាហ្គឹបតា (Brahmagupta polynomial)។ ម៉ាទ្រីសប្រាម៉ាគុបតាអាចពន្លាតជាចំនួនគត់អវិជ្ជមាន ។

និយមន័យ

ពហុធាប៊ែរនូយីគឺជាស្វ៊ីតពហុធាតែមួយគត់ $\left( B_n \right)_{n \in \mathbb{N}}$ ដែល

$B 0 = 1$
$\forall n \in \mathbb{N} , B'_{n+1} = (n+1)B_n$
$\forall n \in \mathbb{N^*} , \int_0 ^1 B_n (x) dx = 0$

[កែប្រែ] អនុគមន៍តំនពូជ

អនុគមន៍តំនពូជ (Generating function) ចំពោះពហុធាប៊ែរនូយីគឺ

$\frac{t e^{xt}}{e^t-1}= \sum_{n=0}^\infty B_n(x) \frac{t^n}{n!}\,$ .

អនុគមន៍តំនពូជ (Generating function) ចំពោះពហុធាអយល័រ (Euler polynomials) គឺ

$\frac{2 e^{xt}}{e^t+1}= \sum_{n=0}^\infty E_n(x) \frac{t^n}{n!}\,$ .

[កែប្រែ] ផលបូកនៃស្វ័យគុណទី p

យើងមាន

$\sum_{k=0}^{x} k^p = \frac{B_{p+1}(x+1)-B_{p+1}(0)}{p+1}$

ចំពោះសេចក្តីលំអិតអំពីរូបមន្តនេះ
សូមមើលរូបមន្តហ្វូលហាប័រ (Faulhaber's formula)

[កែប្រែ] ចំនួនអយល័រ និង ចំនួនប៊ែរនូយី

ចំនួនប៊ែរនូយីអោយដោយ $B_n=B_n(0)\,$ ។
ចំនួនអយល័រអោតយដោយ $E_n=2^nE_n(1/2)\,$ ។

[កែប្រែ] កន្សោមអិចភ្លីស៊ីតចំពោះលំដាប់ទាប

ពហុធាប៊ែរនូយីដំបូងមួយចំនួន

$B_0(x)=1\,$

$B_1(x)=x-1/2\,$

$B_2(x)=x^2-x+1/6\,$

$B_3(x)=x^3-\frac{3}{2}x^2+\frac{1}{2}x\,$

$B_4(x)=x^4-2x^3+x^2-\frac{1}{30}\,$

$B_5(x)=x^5-\frac{5}{2}x^4+\frac{5}{3}x^3-\frac{1}{6}x\,$

$B_6(x)=x^6-3x^5+\frac{5}{2}x^4-\frac{1}{2}x^2+\frac{1}{42}\,$

ពហុធាអយល័រដំបូងមួយចំនួន

$E_0(x)=1\,$

$E_1(x)=x-1/2\,$

$E_2(x)=x^2-x\,$

$E_3(x)=x^3-\frac{3}{2}x^2+\frac{1}{4}\,$

$E_4(x)=x^4-2x^3+x\,$

$E_5(x)=x^5-\frac{5}{2}x^4+\frac{5}{2}x^2-\frac{1}{2}\,$

$E_6(x)=x^6-3x^5+5x^3-3x\,$

[កែប្រែ] ផលសង

ពហុធាប៊ែរនូយី និង ពហុធាអយល័រគោរពតាម
ទំនាក់ទំនងជាច្រើនពីការការគណនានិមិត្តរូប (umbral calculus ឬ symbolic calculus)

$B_n(x+1)-B_n(x)=nx^{n-1}\,$

$E_n(x+1)+E_n(x)=2x^{n}\,$

[កែប្រែ] ដេរីវេ

$B_n'(x)=nB_{n-1}(x)\,$

$E_n'(x)=nE_{n-1}(x)\,$

[កែប្រែ] ការបកប្រែ

$B_n(x+y)=\sum_{k=0}^n {n \choose k} B_k(x) y^{n-k}\,$

$E_n(x+y)=\sum_{k=0}^n {n \choose k} E_k(x) y^{n-k}\,$

[កែប្រែ] ស៊ីមេទ្រី

$B_n(1-x)=(-1)^n B_n(x)\,$

$E_n(1-x)=(-1)^n E_n(x)\,$

$(-1)^n B_n(-x) = B_n(x) + nx^{n-1}\,$

$(-1)^n E_n(-x) = -E_n(x) + 2x^n\,$

[កែប្រែ] លក្ខណៈផ្សេងទៀតនៃពហុធាប៊ែរនូយី

$\forall n \in \mathbb{N}, B_n (x) =2^{n-1} \left( B_n \left( \frac{x}{2} \right) + B_n \left( \frac{x+1}{2} \right) \right)$

[កែប្រែ] តំលៃពិសេស

$\forall n > 1, B_n (0) =B_n (1)$

$\forall p \in \mathbb{N}^{*}, B_{2p+1} (0) = B_{2p+1}(1)=0$

$\forall p \in \mathbb{N}^{*}, B_{2p} \left( \frac {1}{2} \right) = \left( \frac{1}{2^{2p-1}} -1 \right)B_{2p} (0) , B_{2p+1} \left( \frac {1}{2} \right)=0$